Understanding the universal concept behind Kaplan Schoar PME
Do you also feel you missed something important about the famous Kaplan Schoar Public Market Equivalent?
This blog post helps you to understand its success and popularity by addressing the following topics:
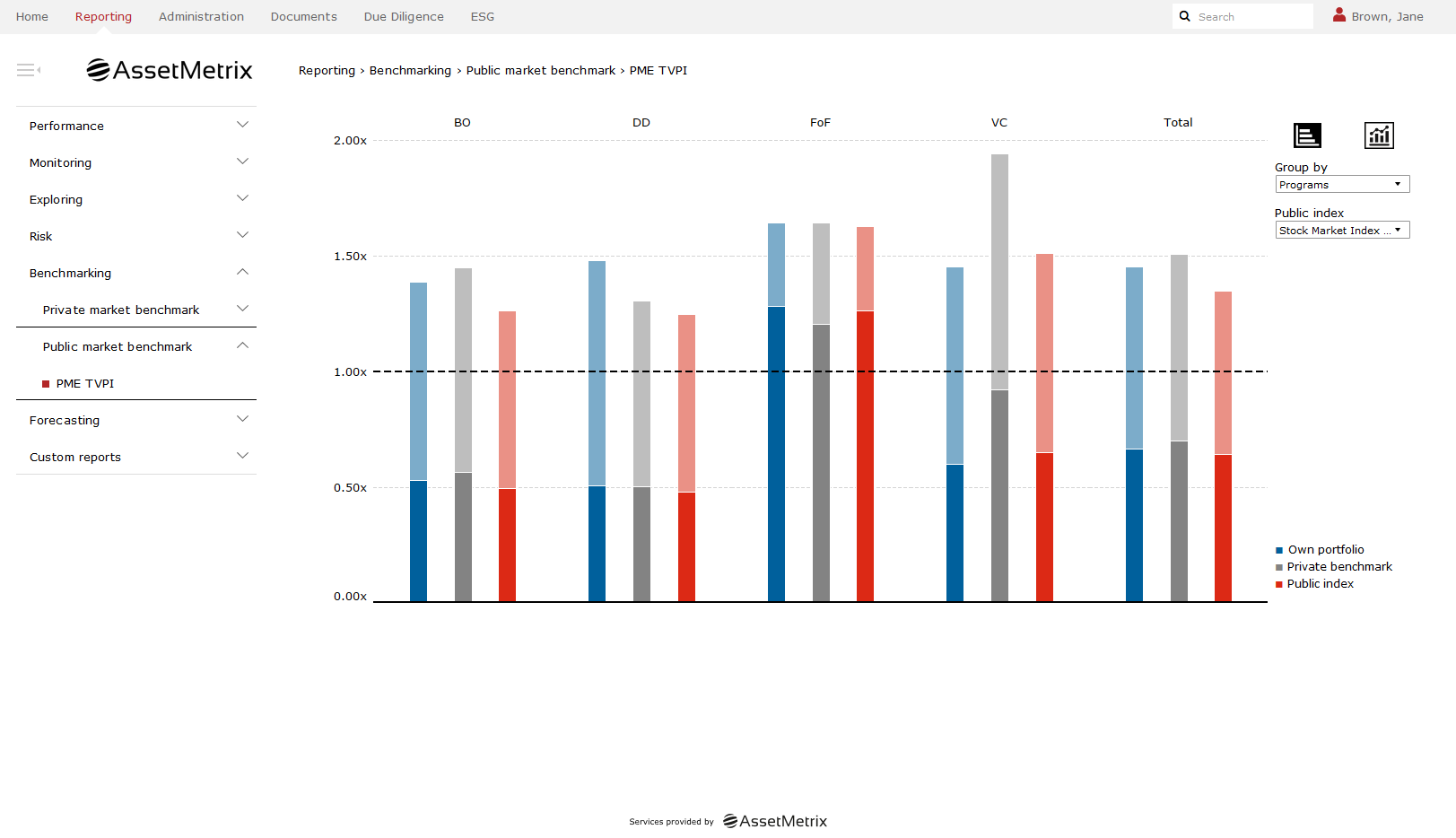
Public Market Equivalent (PME) approaches are developed to measure the investment success of private equity funds in terms of public markets.
Long Nickels (1996) elaborated on the first public market benchmarking method, called the Index Comparison Method (ICM).
More incidentally, Kaplan Schoar (2005) proposed the now-famous KS-PME ratio as “a sensible measure for LPs as it reflects the return to private equity investments relative to public equities”.
Many people believe that these PME approaches of Long Nickels (1996) and Kaplan Schoar (2005) are two rather distinct concepts.
However, Long (2008) showed that both PME measures are based on a common mathematical foundation.
and distribution cash flows by 
for a fully realized private equity fund.
The dates of private equity fund cash flows are denoted by the time index 
.
The public market index we use for benchmarking is denoted by 
.
According to Long Nickels (1996), a private equity fund outperformed the public index, if
![\[ LN-PME = \sum_{t=1}^T \frac{D_t}{I_t} - \sum_{t=1}^T \frac{C_t}{I_t} > 0 \]](https://www.asset-metrix.com/wp-content/ql-cache/quicklatex.com-c7410c8b7f12c07136f5fd591aa28316_l3.png "Rendered by QuickLaTeX.com")
![\[ KS-PME = \frac{ \sum_{t=1}^T \frac{D_t}{I_t} }{ \sum_{t=1}^T \frac{C_t}{I_t} } > 1 \]](https://www.asset-metrix.com/wp-content/ql-cache/quicklatex.com-90dc5062fb8fce52c327d43231d02616_l3.png "Rendered by QuickLaTeX.com")
Many people share the concern that both approaches lack a systematic risk adjustment. However, Sorensen Jagannathan (2015) discussed why systematic risk adjustments are unnecessary under relatively mild assumptions.
The general validity of those PME methods originates from a financial mathematics concept called ‘numeraire denomination’.
Numeraire denomination is one of the most essential and universal concepts that financial mathematicians apply (almost) all the time.
The idea behind numeraire denomination is strikingly simple: divide all cash flows, security prices, etc. that appear in a financial model by a (default-free) public index. To satisfy the next fundamental concept in financial mathematics called ‘martingale property’, you should choose a broadly diversified public index as the denominator.
That’s it!
Kaplan Schoar (2005) PME is really straightforward and very similar to the Long Nickels (1996) approach: divide all private cash flows you encounter by a broad public index, as all financial economists and mathematicians approve it!
And in consequence, as the method is easy to implement and understand, all practitioners should likewise embrace it!
Of course, it is also a vital component of the AssetMetrix benchmarking module!
Christian Tausch
Analytics
puevfgvna.gnhfpu@nffrg-zrgevk.pbz
Need more information?
To learn more about our benchmarking solutions, please contact our team.
Request meeting!
Further Analytics Insights
As evidenced by recent EU regulations, Liquidity Stress Testing (LST) is a vital topic for Alternative Investment Fund Managers (AIFMs). Find out more about LST solutions.
Liquidity planning and management continue to be crucial topics for private capital funds. In this article, we provide insights on how a sophisticated tool can simplify your planning.
Due to the illiquidity of private capital funds, it is of utmost importance for investors, but also for fund managers, to know exactly the cash flow profile of their portfolio or funds. In the following, we describe our innovative cash flow forecasting engine that facilitates this.
This paper discusses why proper risk measurement for private capital funds is notoriously difficult and how to overcome these challenges.